A new method called subset optimisation long (SOL) improves how portfolios and indices are built to achieve the highest risk-adjusted returns, the objective of all rational investors.
SOL addresses the limitations of existing methods like the Capital Asset Pricing Model (CAPM) and Markowitz's mean-variance optimisation when used in real-life scenarios. For instance, CAPM's assumptions about market efficiency do not work well in practice. Markowitz's method is powerful but becomes less accurate when there are many different securities.
In contrast, SOL consistently produces higher risk-adjusted returns compared to other methods. It is also great for creating custom indices with superior returns without extra calculations.
Markowitz's Modern Portfolio Theory (MPT) is a framework for building portfolios that maximise expected returns for a given level of risk. MPT introduces the concept of the "efficient frontier," representing the portfolio with the highest expected return for any given risk level. It also shows that there is an optimal combination of assets that offers the single best trade-off between risk and return.
Bill Sharpe expanded on Markowitz's work with the Capital Asset Pricing Model (CAPM) and introduced the concept of the market portfolio, the portfolio that contains all risky assets in the market, weighted according to their market values. It represents the collective investment universe and is assumed to be efficient in the sense that it provides the highest risk-adjusted return (i.e., it represents the optimal combination of assets).
However, CAPM's validity and assumptions are still debated. Its assumptions that there are no transaction costs, all investors have the same horizon, and all securities have similar liquidity don’t match real-world scenarios. The CAPM also assumes that markets are perfectly efficient, meaning all relevant information is instantly reflected in asset prices and that a security’s beta, a measure of systematic risk, is the sole determinant of a security’s return. However, empirical research has shown that markets are not always efficient, as there can be instances of market anomalies and inefficiencies that generate abnormal returns.
Additionally, systematic risk is not always the best determinant of return. As a result, proposed indices and weighting schemes, like market capitalisation-weighted equity indices, and the standard proxy, have not fully resolved these issues as they have been shown to not offer the best risk/return trade-off.
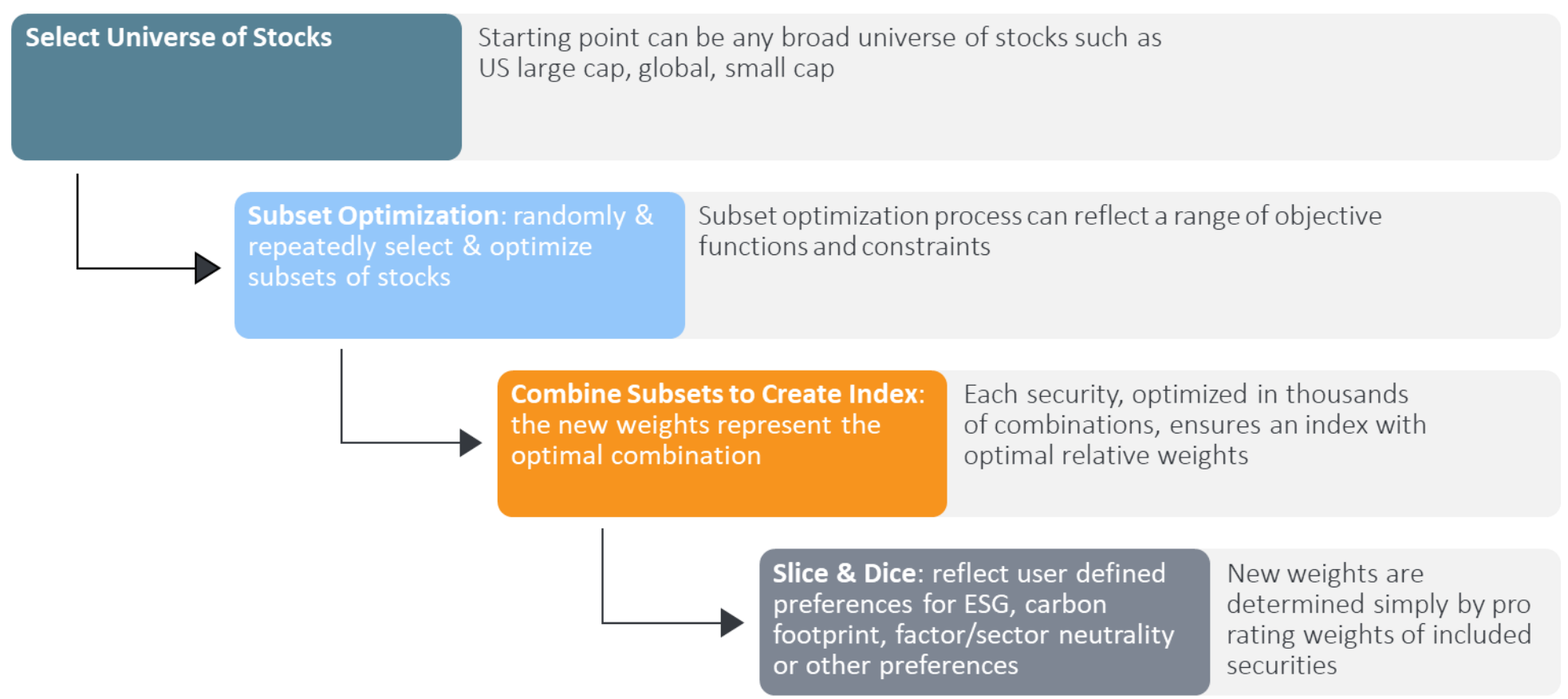
To address these limitations, Professor Ben Gillen of Claremont McKenna University, in partnership with Parala Capital, has developed SOL, a novel method for portfolio and index construction. In its most straightforward form, SOL simplifies the optimisation process when considering many securities by instead of trying to optimise the entire universe at once, focusing on smaller, randomly selected subsets of securities. For each of the thousands of randomly selected subsets, it optimises the weights (i.e., the proportion of investment) of the securities. These subsets are combined to form an index with optimal security weights, minimising estimation errors and increasing diversification for better risk-adjusted returns.
Why are the weights of the securities optimal? Imagine a single security like Amazon. The SOL methodology calculates the optimal weight of Amazon in thousands of separate combinations of securities. When these optimised subsets are recombined, it is highly likely that the derived weight of Amazon is its optimal weight.
Chart 1: SOL represents a novel approach to constructing optimal indices
Source: Parala Capital
What further distinguishes SOL is its capacity to allow investors to choose any combination of securities and optimally adjust their weights to maximise risk-adjusted returns. This is facilitated by SOL's ability to proportionally scale the weights of securities, independent of each other. Essentially, by simply adjusting the weights, investors can achieve an optimal combination that yields the highest expected risk-adjusted return.
As a result, indices developed using SOL maintain the essential characteristics of traditional indices, but with the added benefit of potentially higher risk-adjusted returns.
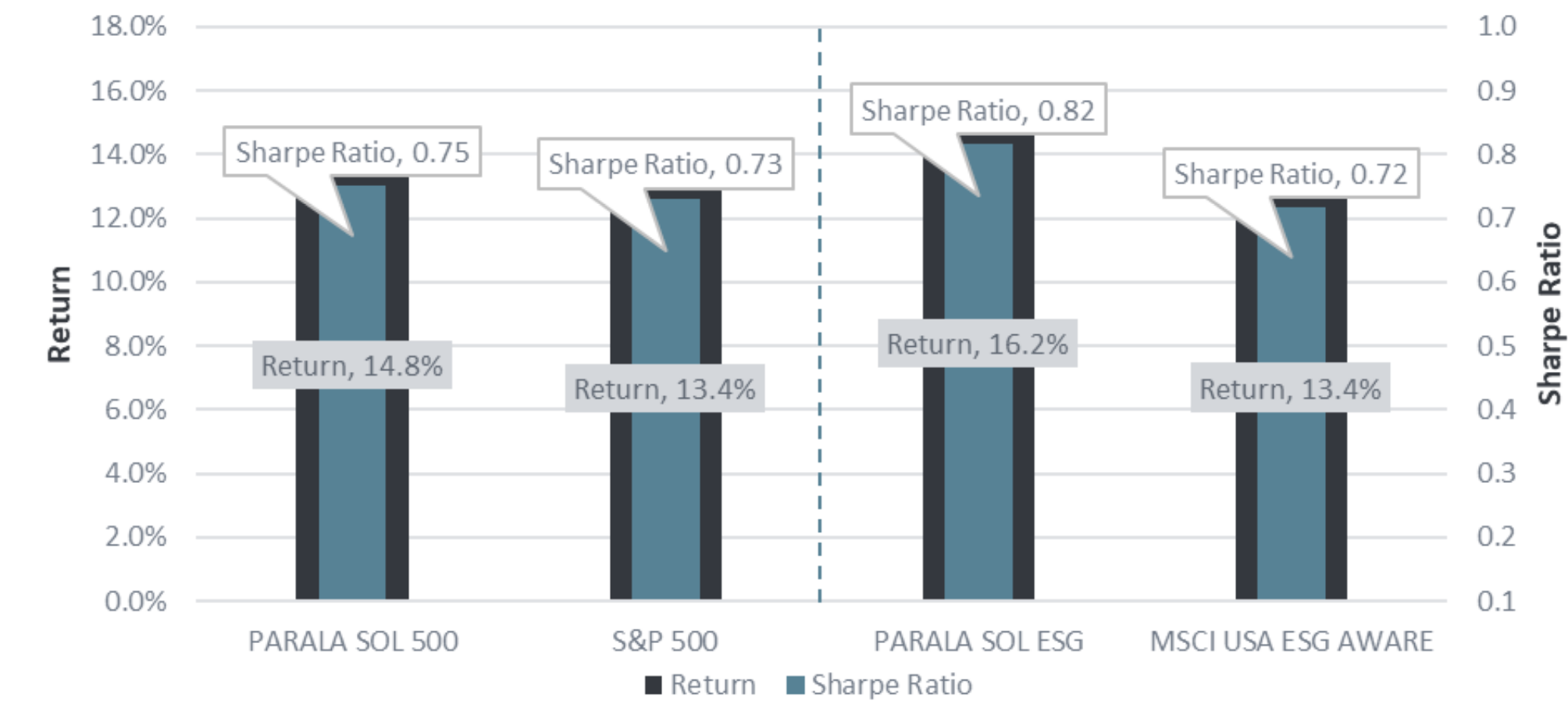
Chart 2: Annualised returns and risk-adjusted returns – seven years ending June
Source: Parala Capital
This means the SOL methodology has significant implications for investment strategies and index construction.
Applying SOL to large-cap US equities, for example, can result in higher risk-adjusted returns compared to conventional indices. This concept can be extended to various solutions, accommodating specific investor preferences, including value, growth, momentum, ESG, and custom index strategies, which can accommodate granular investor preferences. In each instance, utilising the same optimal security weights, simply pro-rated, can lead to higher risk-adjusted returns, all without requiring additional computational efforts.
Reza Vishkai is a founding partner at Parala Capital



